| Definitions | t  T, {T}, P T, {T}, P   Q, Q,  x:A. B(x), SQType(T), loc(e), s ~ t, P x:A. B(x), SQType(T), loc(e), s ~ t, P  Q, x:A Q, x:A  B(x), B(x),  b, ES, Type, IdLnk, Atom$n, Id, a:A fp b, ES, Type, IdLnk, Atom$n, Id, a:A fp B(a), B(a),  x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v), @i discrete ds, x:A P(x;v), @i discrete ds, x:A  B(x), B(x),  e@i. P(e), False, s = t, (e <loc e'), (e < e'), e@i. P(e), False, s = t, (e <loc e'), (e < e'),  A, e A, e  loc e' , e c loc e' , e c e', t.1, E, State(ds), e', t.1, E, State(ds),  , <a, b>, , <a, b>,  , {x:A| B(x)} , vartype(i;x), Top, f(x)?z, Knd, valtype(e), , {x:A| B(x)} , vartype(i;x), Top, f(x)?z, Knd, valtype(e), 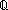 , A c , A c B, left + right, P & Q, B, left + right, P & Q,  x:A. B(x), discrete state@i, (discrete state after e), isrcv(e), if b then t else f fi , x,y:A//B(x;y), True, f(a), x:A. B(x), discrete state@i, (discrete state after e), isrcv(e), if b then t else f fi , x,y:A//B(x;y), True, f(a),  T, T,  , ,   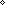 , A , A 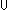 B, EquivRel(T;x,y.E(x;y)), tt, qeq(r;s), B, EquivRel(T;x,y.E(x;y)), tt, qeq(r;s),   x,y. t(x;y), sender(e), let x,y = A in B(x;y), source(l), Void, locl(a), P x,y. t(x;y), sender(e), let x,y = A in B(x;y), source(l), Void, locl(a), P   Q, P Q, P    Q, Unit, case b of inl(x) => s(x) | inr(y) => t(y), Q, Unit, case b of inl(x) => s(x) | inr(y) => t(y), 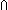 x:A.B(x), rcv(l,tg), kind(e), Dec(P), discrete-weak-precond-send-p(es;T;A;l;tg;a;ds;P;f), weak-precond-send-p(es;T;A;l;tg;a;ds;P;f), x:A.B(x), rcv(l,tg), kind(e), Dec(P), discrete-weak-precond-send-p(es;T;A;l;tg;a;ds;P;f), weak-precond-send-p(es;T;A;l;tg;a;ds;P;f),   x. t(x), state@i, (state when e), (state after e)+t, state after e x. t(x), state@i, (state when e), (state after e)+t, state after e |